Leerdoel: het kunnen rekenen met percentages, breuken en decimale getallen en snappen dat ze allen dezelfde deel van het geheel zijn.
Wat betekent dit nou eigenlijk?
Percentages, breuken en kommagetallen (decimalen) lijken misschien verschillend, maar ze betekenen eigenlijk hetzelfde: een deel van een geheel.
Bijvoorbeeld:
- 25% = ¼ = delen door 4
- 50% = ½ = delen door 2
- 12,5% = 1/8 = delen door 8
In groep 8 leer je hoe je kunt kiezen tussen die vormen om een som makkelijker te maken. Je leert dus:
- Rekenen met een percentage als breuk (bijv. 25% van 60 = ¼ van 60)
- Rekenen met een percentage als kommagetal (bijv. 40% van 60 = 0,4 × 60)
Je kiest de vorm die jij het handigst vindt. Dat helpt je om flexibel te rekenen én om beter te snappen hoe getallen met elkaar samenhangen.
Voorbeeld 1: 25% van 60
Manier 1: naar breuken gaan (klik hier voor de gehele lijst)
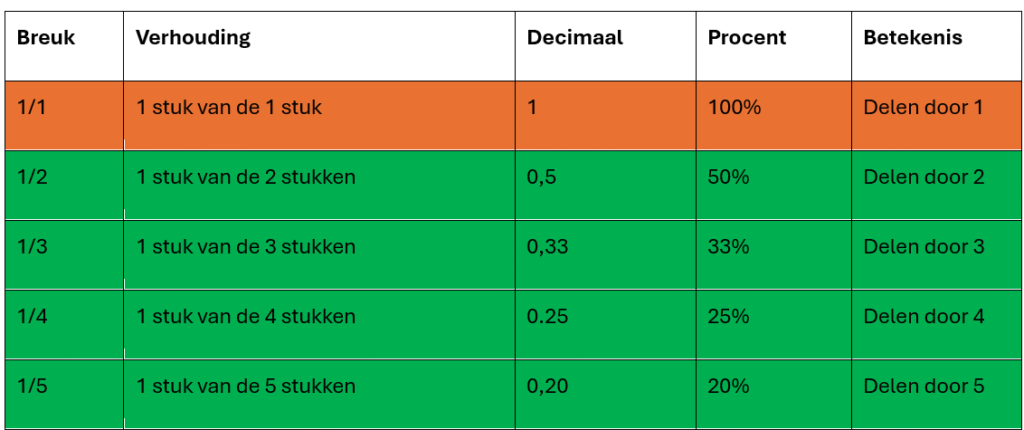
Je weet:
25% = ¼
Dus:
➤ ¼ van 60 = 60 ÷ 4 = 15
✅ Antwoord: 25% van 60 is 15
Oefeningen voor begrip
Oefenvragen – Breuk, Decimaal en Procent
- 1/2 van 60 = ?
A. 20 B. 25 C. 30 D. 40 - 0,25 x 80 = ?
A. 10 B. 15 C. 20 D. 25 - 20% van 45 = ?
A. 7 B. 8 C. 9 D. 10 - 1/5 van 50 = ?
A. 8 B. 9 C. 10 D. 12 - 0,5 x 18 = ?
A. 6 B. 8 C. 9 D. 12 - 25% van 32 = ?
A. 6 B. 7 C. 8 D. 9 - 1/4 van 12 = ?
A. 2 B. 3 C. 4 D. 6 - 0,2 x 70 = ?
A. 10 B. 12 C. 14 D. 15 - 10% van 90 = ?
A. 7 B. 8 C. 9 D. 10 - 0,33 x 60 ≈ ?
A. 15 B. 18 C. 20 D. 22
Antwoorden en uitleg
- C – 30 → 1/2 = delen door 2 → 60 ÷ 2 = 30
- C – 20 → 0,25 = 1/4 = delen door 4 → 80 ÷ 4 = 20
- C – 9 → 20% = 1/5 = delen door 5 → 45 ÷ 5 = 9
- C – 10 → 1/5 = delen door 5 → 50 ÷ 5 = 10
- C – 9 → 0,5 = 1/2 = delen door 2 → 18 ÷ 2 = 9
- C – 8 → 25% = 1/4 = delen door 4 → 32 ÷ 4 = 8
- B – 3 → 1/4 = delen door 4 → 12 ÷ 4 = 3
- C – 14 → 0,2 = 1/5 = delen door 5 → 70 ÷ 5 = 14
- C – 9 → 10% = 1/10 = delen door 10 → 90 ÷ 10 = 9
- C – 20 → 0,33 ≈ 1/3 = delen door 3 → 60 ÷ 3 = 20