Leerdoel 1F: De leerling kan een deel van een geheel of een deel van een hoeveelheid uitdrukken in een breuk, bij eenvoudige verhoudingen en elementaire breuken (zoals ½, ⅓, ¼, 1⁄5, etc.) en bij ronde aantallen in herkenbare situaties. Ook schattend of ongeveer redeneren met breuken hoort hierbij.
Leerdoel 1S: De leerling moet ook minder eenvoudige getallen dan bij 1F genoemd worden en in meer formele opgaven dit kunnen.
Wat betekent dit nou eigenlijk?
Een leerling moet snappen dat bijvoorbeeld een deel van een groep of een stuk van een pizza in plaats van een percentage of getal, uitgedrukt kan worden in een breuk.
Bijvoorbeeld:
- 8 van de 24 kinderen → dat is een deel van de klas → je drukt dat uit als een breuk van het totaal
- Je leert dan schrijven: 8⁄24, en dat eventueel vereenvoudigen naar 1⁄3.
Je leert ook dat 60 op de 120 kinderen betekent: 60⁄120 → dat is de helft, oftewel ½.
Voorbeeld 1 (1F)
Opdracht: In groep 3 zitten 24 kinderen. 8 kinderen zitten op zwemles.
Vraag: Welk deel van de klas is dat?
Uitwerking: rekenmachine-manier
- 8 ÷ 24 = 0,333…
- Dat is ⅓ → 8⁄24 kun je vereenvoudigen door teller en noemer te delen door 8 → 1⁄3
Uitwerking: zodat je het snapt
- Er zijn 24 kinderen in totaal
- 8 kinderen doen mee → je schrijft dat als 8⁄24 (acht van de 24)
- Je deelt beide getallen door 8: 8 ÷ 8 = 1 en 24 ÷ 8 = 3 → Dus: 1⁄3 van de klas zit op zwemles. (vereenvoudigen -> zie hieronder)
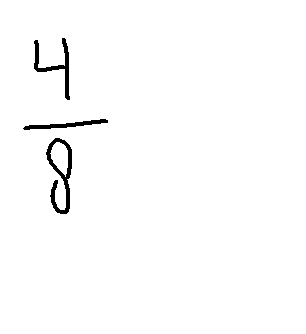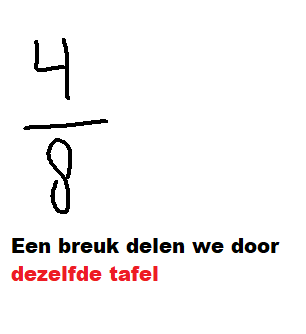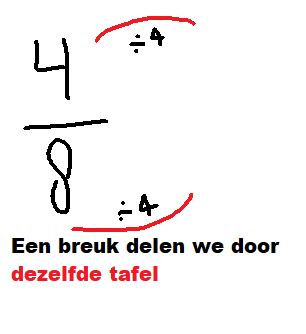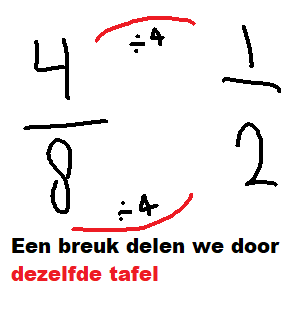
Voorbeeld 1 (1S)
Opdracht: 18 van de 27 kinderen zitten op zwemles.
Vraag: Welk deel van de klas is dat?
Uitwerking: rekenmachine-manier
- 18 ÷ 27 = 0,666… → dat is 2⁄3
Uitwerking: zodat je het snapt
- Je maakt er een breuk van: 18⁄27
- Beide getallen deelbaar door 9: 18 ÷ 9 = 2, 27 ÷ 9 = 3
→ 18⁄27 = 2⁄3 van de klas zit op zwemles